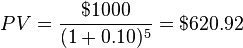Project selection methods:
With a profusion of interesting, challenging projects to choose from, finding a project that is the right fit for your team's skill set and level of competence and affords the best chance of success is the first step in successful project management. Project Selection Methods offer a set of time-tested techniques based on sound logical reasoning to arrive at a choice of project, and filter out undesirable projects with very low likelihood of success. This is an important concept for project management professionals for the PMP exam as well as the applications in an organization.

What Are Project Selection Methods?
Consider a scenario in which the organization you are working for has been given access to a number of projects. But due to constraints of resources, the organization cannot take up all the projects at once. Therefore, a decision has to be made as to which project needs to be taken up that will provide maximum profit and recognition.
This is where Project Selection Methods come into play. These can be divided into two categories, namely:
Benefit Measurement Methods - used for small and non complex projects.
Constrained Optimization Methods - used for complex and large projects. A detailed discussion of these topics is out of the scope of the PMP Certification exam. For the exam, all you need to know is that these are the Mathematical Model techniques and are used in project selection.
Benefit Measurement Methods
Murder board - a panel of people trying to shoot down ideas.
Peer review
Scoring model
Economic models
Economic models: Economic models take a comparative approach for project selection & fall into the category of benefit measurement.
Benefit-Cost analysis
Present Value
Net Present Value
IRR
Payback period
Benefit-Cost Ration (BCA) - Project with Higher BCA will be selected.
Economic Value Added (EVA) - Project with Higher Economic Value Add will be selected.
Net Present Value (NPV) - Project with the Higher NPV will be a better option.
Internal Rate of Return (IRR) - Project with Higher IRR will be selected.
Payback Period - Project with the minimum payback period will be selected.
Scoring Model - Project with Higher score will be selected.
Discounted Cash Flow - Project with Higher DCF will be selected.
Opportunity cost - If you have many projects, you will chose the project with the lesser opportunity cost.
Note: Only Payback and Opportunity cost methods have - lesser is better.
Refer to
http://wps.pearsoncustom.com/wps/media/objects/7225/7398617/MGT310_Ch03.pdf
or Read this document
Benefit-Cost Ration (BCA) - Project with Higher BCA will be selected.
Economic Value Added (EVA) - Project with Higher Economic model will be selected.
Net Present Value (NPV) - Project with the higher NPV will be a better option.
Scoring Model - Project with highest score will be selected.
Discounted Cash Flow - Project with higher DCF will be selected.
Internal Rate of Return (IRR) - Project with higher IRR will be selected.
Payback Period - Project with the minimum payback period will be selected.
Opportunity cost - If you have many projects, you will chose the project with the lesser opportunity cost.
Cost-benefit analysis (CBA)
AKA Benefit-Cost Ration (BCA) - Project with Higher BCA will be selected.
It is sometimes called benefit–cost analysis (BCA), is a systematic approach to estimating the strengths and weaknesses of alternatives.
Broadly, CBA has two purposes:
To determine if it is a sound investment/decision (justification/feasibility),
To provide a basis for comparing projects. It involves comparing the total expected cost of each option against the total expected benefits, to see whether the benefits outweigh the costs, and by how much.[1]
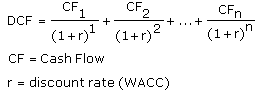
=====================================================================
The formula for NPV is:
NPV = Present value (PV) of cash inflows (positive) + present value (PV) of cash outflows (negative)
If NPV is positive, that's good. You can consider the project for selection.
If NPV is negative, it's bad. The project shouldn't be considered for selection.
Net Present Value (NPV) - Project with the higher NPV will be a better option.
====================================================================
I. The Definition of IRR
Internal rate of return is the interest rate (or discount rate) at which the net present value for the project is zero.
In other words, the rate at which cash inflows equal cash outflows is considered as internal rate of return. It's called "internal rate of return," because there are no other external influences or environmental factors.
As the cash inflows equal cash outflows, for IRR the NPV for the project will be zero. If we put it mathematically, the equation would be:
NPV = 0
=> PV of cash inflows for the project (positive) + PV of cash outflows for the project (negative) = 0
=> PV cash inflows for the project = PV cash outflows for the project
The rate at which present value of cash inflows equals PV of cash outflows will be the IRR. IRR is always noted in percentage terms. To understand, let's look at an example.
An Example of IRR
Your organization has an investment of $100,000 for a project. After one year you will get $110,000 in return. Calculate the IRR.
Present value (PV) of cash outflows for the project = $100,000
Future Value (FV) of cash inflows for the project = $110,000
It's called future value, because we'll get the money after one year.
Therefore, PV of cash inflows for the project = $110,000/(1+R), where R is the rate of return or discounted rate.
For IRR, the value of NPV is zero.
=>PV of cash inflows = PV cash outflows
=> $110,000/(1+R) = $100,000
=> 1 + R = $110,000/$100,000
=> R = ($110,000/$100,000) - 1 = $10,000/$100,000 = 1/10
Or R in percentage terms = (1/10) * 100 = 10%
The IRR for the project is 10 percent.
Let's say you've received the capital of $100,000 at a rate of 12 percent from the investor. After all, someone -- internal or external -- will need to invest in the project. That investor will be expecting a return out of it. This rate is called Cost of Capital (CoC) in accounting terms, because there's a cost associated with it. You have to provide a return for this capital.
However, as you found out above, your IRR is coming at 10 percent, while your CoC is at 12 percent. Will you go for the project? Obviously not. You wouldn't be making any money out of it by executing this project. This leads us to an important conclusion in project selection while using IRR.
If IRR is greater than the desired cut-off rate (or CoC), then you will go ahead with the project.
If IRR is less than the desired cutoff rate (or CoC), then you won't proceed.
II. Ways to Calculate IRR
IRR can be calculated in two ways: for uniform cash flows and for non-uniform cash flows.
II.1: IRR Calculation for Uniform Cash Flows
In the previous example, I showed a simple project with a one-time investment. However, for uniform cash inflows -- a series of cash flows that's uniform year after year, IRR is calculated considering the annuity discount factor.
The formula for annuity discount factor is:
Project investment = Annual net cash flow * Annuity discount factor
=>Annuity discount factor = Project investment/Annual net cash flow
Annuity is a fixed sum of money to be paid every year as a series of payments. (This is another accounting term.)
Once the annuity discount factor is calculated, annuity table is referred to find IRR. Annuity tables are available on accounting sites. If this topic surfaces on your exam, it'll probably reference the present value of annuity factors.
Example 2: Annuity Factors
For this example, I've modified the first example. You have a $100,000 investment for a project. After one year you expect $110,000 in return. Find out the IRR with the help of the annuity factor.
The annuity factor table is given below.
In this case, there is one-time investment and a return is mentioned for one year. I have put that into a table as shown below. Note that cash inflows are mentioned as positive, whereas cash outflows are negative, highlighted in red and put in parentheses.
Annuity discount factor = Project investment/Annual net cash flow
=> Annuity discount factor = $100,000/$110,000
=> Annuity discount factor = 10/11 = 0.9090 = 0.9091(approx.)
Looking at the above annuity discount factor table (given in the question), we have a rate of 10 percent for an annuity factor of 0.9091. So the IRR for this project is 10 percent.
Now, let us change this example a bit, to examine annual uniform cash flow.
Example 3: Annual Uniform Cash Flow
You have a $100,000 investment for a project. The expected return on the project in its useful life is $125,000. The useful life of the project is five years. The cash inflow is expected to be uniform. Find out the IRR. The annuity table is shown below.

Here, the cash flow is uniform. Considering the cash inflows and cash outflows, we have the following table. As we have $125,000 over a period of five years, for each year the cash inflow will be $25,000. Note that cash inflows are mentioned as positive, whereas cash outflows (investment) are negative.
Project investment = $100,000 and Annual net cash flow = $25,000
Hence, Annuity Discount Factor = Project Investment/Annual Net Cash flow
= $100,000/$25,000
= 100/25 = 4, which is close to 3.9927.
For the annuity discount factor of 3.9927, looking up the table shown in the question, the rate comes out to be at 8 percent. Hence IRR for the project is 8%.
II.2: IRR Calculation for Non-uniform Cash FlowsFor non-uniform or uneven cash flow, we have to calculate the IRR in a different way. First, we need to find out the average cash flow in a year, from which we derive the annuity discount factor. Then, looking up the annuity table, we get an approximate value of IRR. From there, by trial and error and interpolation, the final IRR is derived.
In an uneven cash flow scenario, the formula for IRR is:

It doesn't matter if you have NPV or PV in the denominator. The final value of IRR will remain the same. Both formulas above are correct for IRR.
It's unlikely that you'll have questions about this in the PMP exam. But I've put the formula in in case you're wondering what happens if there's uneven cash flow.
III. IRR for Mutually Exclusive ProjectsIRR can be used to make selection decision between two or more independent projects. The general rule followed for IRR: The higher the better. In other words, all other things being equal, the project with the highest IRR should be selected. Let's take another example to understand this concept.
Example 4: Choosing Between Projects based on IRR
There are four projects before the selection committee, out of which only one can be selected. The IRR for each project is shown below. Which one will be chosen?
Answer:
The project with the highest IRR will be chosen. Above, that’s project B with an IRR of 42 percent.
However, there’s a note of caution when mutually exclusive projects are involved. If both NPV and IRR are present, it’s a good idea to look for NPV as well. A project with higher IRR but lower NPV wouldn’t be preferable over a project with a lower IRR but higher NPV.
To illustrate, here’s an example.

For project A, NPV = - $1,000 + $2,100 = $1,100
For project A, we have to make NPV zero to find out IRR.
=> - $1,000 + [($2,100)/(1+IRR)] = 0
=> 1 + IRR = 2,100/1,000 = 2.1 => IRR = 2.1 – 1 = 1.1
=> IRR = 110%
Above, I have applied the simple formula, as outlined before, to calculate the IRR. I can also look at the annuity table to derive the IRR.
For project B, NPV = - $10,000 + $15,000 = $5,000
For project B, we have to make NPV zero to find out IRR.
=> - $10,000 + [($15,000)/(1+IRR)] = 0
=> 1 + IRR = 15,000/10,000 = 1.5 => IRR = 1.5 – 1 = 0.5
=> IRR = 50%
Now, which one to choose?
• Project A higher IRR (110%), but lower NPV ($1,100)
• Project B lower IRR (50%), but higher NPV ($5,000)
Project B will be selected as it gives maximum value to the stakeholders or has higher wealth maximization.
Finally, let us look at the advantages and disadvantages of IRR to have needed understanding on it for the PMP exam.
IV. Advantages and Disadvantages for IRR:

With a profusion of interesting, challenging projects to choose from, finding a project that is the right fit for your team's skill set and level of competence and affords the best chance of success is the first step in successful project management. Project Selection Methods offer a set of time-tested techniques based on sound logical reasoning to arrive at a choice of project, and filter out undesirable projects with very low likelihood of success. This is an important concept for project management professionals for the PMP exam as well as the applications in an organization.
What Are Project Selection Methods?
Consider a scenario in which the organization you are working for has been given access to a number of projects. But due to constraints of resources, the organization cannot take up all the projects at once. Therefore, a decision has to be made as to which project needs to be taken up that will provide maximum profit and recognition.
This is where Project Selection Methods come into play. These can be divided into two categories, namely:
Benefit Measurement Methods - used for small and non complex projects.
Constrained Optimization Methods - used for complex and large projects. A detailed discussion of these topics is out of the scope of the PMP Certification exam. For the exam, all you need to know is that these are the Mathematical Model techniques and are used in project selection.
Benefit Measurement Methods
Murder board - a panel of people trying to shoot down ideas.
Peer review
Scoring model
Economic models
Economic models: Economic models take a comparative approach for project selection & fall into the category of benefit measurement.
Benefit-Cost analysis
Present Value
Net Present Value
IRR
Payback period
Benefit-Cost Ration (BCA) - Project with Higher BCA will be selected.
Economic Value Added (EVA) - Project with Higher Economic Value Add will be selected.
Net Present Value (NPV) - Project with the Higher NPV will be a better option.
Internal Rate of Return (IRR) - Project with Higher IRR will be selected.
Payback Period - Project with the minimum payback period will be selected.
Scoring Model - Project with Higher score will be selected.
Discounted Cash Flow - Project with Higher DCF will be selected.
Opportunity cost - If you have many projects, you will chose the project with the lesser opportunity cost.
Note: Only Payback and Opportunity cost methods have - lesser is better.
Refer to
http://wps.pearsoncustom.com/wps/media/objects/7225/7398617/MGT310_Ch03.pdf
or Read this document
Benefit-Cost Ration (BCA) - Project with Higher BCA will be selected.
Economic Value Added (EVA) - Project with Higher Economic model will be selected.
Net Present Value (NPV) - Project with the higher NPV will be a better option.
Scoring Model - Project with highest score will be selected.
Discounted Cash Flow - Project with higher DCF will be selected.
Internal Rate of Return (IRR) - Project with higher IRR will be selected.
Payback Period - Project with the minimum payback period will be selected.
Opportunity cost - If you have many projects, you will chose the project with the lesser opportunity cost.
Cost-benefit analysis (CBA)
AKA Benefit-Cost Ration (BCA) - Project with Higher BCA will be selected.
It is sometimes called benefit–cost analysis (BCA), is a systematic approach to estimating the strengths and weaknesses of alternatives.
Broadly, CBA has two purposes:
To determine if it is a sound investment/decision (justification/feasibility),
To provide a basis for comparing projects. It involves comparing the total expected cost of each option against the total expected benefits, to see whether the benefits outweigh the costs, and by how much.[1]
As
the name suggests, it is the ratio between the present value of inflow
(cost invested to the project) and present value of outflow (value of
return form the project). If the budget is not a constraint, the project
with higher Benefit-Cost Ratio (BCR) will be selected.
Let's
start by reviewing one of the simpler techniques, which is Benefit Cost
Analysis. Here we want to determine the overall financial benefit of
the project (the total amount of money it will generate) and compare
that figure to what we must spend to complete the project.
Thus,
if a project costs $1 million dollars to perform, but will return $1.5
million in proceeds, the benefit cost ratio is 3:2, meaning it will
return $3 for every $2 invested. This ratio can then be reduced by
dividing the benefit value by the cost value (here, 3/2). In this case,
the benefit cost ratio can also be expressed as 1.5, meaning we realize
$1.50 in returns for every $1 invested. This provides a good indicator
of the project's economic viability, but it often does not include the
discounted value of the returns (i.e. what the future income is worth in
today's dollars, after adjusting for interest and inflation). To
provide the most meaningful figures, therefore, the future income should
be appropriately discounted before it is compared to the amounts we
must spend up front in order to do the project.
Economic Value Added (EVA) - Project with Higher Economic model will be selected.
Economic
Value Added (EVA) is a performance metric that calculates the worth
creation for the organization, and defines the return on capital (ROC).
It is the net profit after deducting all taxes and capital expenditure.
If
you have many projects, the project with the higher Economic Value
Added (EVA) will be selected. Keep in mind that EVA is expressed in
dollar value, not in a percentage.
Scoring Model - Project with highest score will be selected.
This
is more like an objective technique. Here, the project selection
committee will list a few relevant criteria, weigh them according to
their priorities and importance, and then will add all these weighted
values.
Once you complete scoring the projects, the project with highest score will be selected.
Moving
away from the strict financial analyses, another helpful way to
evaluate potential projects is to rate them on various weighted
criteria, and come up with an overall score. For example, let's choose 5
criteria that are important to us (we will use profitability, technical
difficulty, resource strain, risk and stakeholder support for this
example).
We then want to weigh these various criteria
so that they collectively add up to 100%. So let's say profitability is
the most important, so we give it a 40% weight. Next up is technical
difficulty, at 20%, followed by resource strain, at 15%, with risk also
being weighted at 15% and stakeholder support coming in at 10%.
Next
we need to determine how each project scores on these various rankings.
We want to identify some consistent values to use here, to ensure the
raw scores assigned for each attribute add up to 100 across all
projects. For example, if we have 5 possible projects, we might use
predetermined scores of, say, 5, 10, 20, 25 and 40, to ensure they
collectively will add up to 100 (this aligns with our weighting figures,
which also add up to 100).
We then analyze each
possible project by multiplying its score for each criterion by the
percentage weight that criterion was assigned in order to get a weighted
score for that particular project attribute. Let's assume Project A
seems highly profitable, so we give it a score of 40 in the
profitability column. That 40 then gets multiplied by .4, since we
weight the profitability attribute at 40% of the total concern. The
combined score for profitability would then be 16.
We
then repeat this process for each criterion, and add up the 5 weighted
scores to get a total score for Project A. These steps are then repeated
for all other project options, to identify the potential project which
gets the highest overall score.
This technique is
especially useful in cases where organizations place a particularly
heavy emphasis on one particular project aspect or constraint.
Naturally, these tendencies may change over time. If the organization is
currently understaffed, for example, then resource strain will likely
be weighted most heavily.
Apart from its ability to
weight key concerns as part of the overall score, this technique is also
popular because it provides a highly objective way of analyzing
potential project options. Once the weights and scores are assigned, we
simply let the math decide which project should be chosen.
Payback Period - Project with the minimum payback period will be selected.
This
is the ratio of total cash out with average per period cash in. Or you
can say that it is the time required to recover the cost invested in the
project.
If other parameters are the same, the project with the minimum payback period will be selected.
Another
simple technique one might use is called Payback Period, where we
determine the amount of time it will take to recoup our initial
investment from a project. For example, if we project to spend $500,000
to perform a project, and expect it will return revenue at the rate of
$50,000 per year, our payback period would be 10 years (measured from
the date of project completion).
But as with the
Benefit Cost Analysis, our results here can be misleading because they
typically do not factor in the time value of money. Yes, we will
ultimately recover $500,000 over 10 years, but that does not equal
$500,000 in today's money (because inflation and cost of capital are not
usually factored in). We therefore are not really comparing "apples to
apples," since the present value of that future revenue stream is
actually much less than $500,000 once we discount that figure to present
day values.
Discounted Cash Flow: Project with higher DCF will be selected.
A valuation method used to estimate the attractiveness of an investment opportunity. Discounted cash flow (DCF) analysis uses future free cash flow projections and discounts them (most often using the weighted average cost of capital) to arrive at a present value, which is used to evaluate the potential for investment. If the value arrived at through DCF analysis is higher than the current cost of the investment, the opportunity may be a good one.
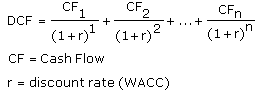
=====================================================================
The formula for NPV is:
NPV = Present value (PV) of cash inflows (positive) + present value (PV) of cash outflows (negative)
If NPV is positive, that's good. You can consider the project for selection.
If NPV is negative, it's bad. The project shouldn't be considered for selection.
Net Present Value (NPV) - Project with the higher NPV will be a better option.
This is the difference between the current value of cash inflow and the current value of cash outflow of the project. Net Present Value (NPV) should always be positive, and the project with the higher NPV will be a better option.
Because the value of revenue earned today is higher than that of revenue earned down the road, businesses discount future income by the investment's expected rate of return. This rate, called the hurdle rate, is the minimum rate of return a project must generate for the business to consider investing in it.
Present Value - (PV)
The PV calculation indicates the discounted value of all revenue generated by the project, while the NPV indicates how profitable the project will be after accounting for the initial investment required to fund it.
For example, if you are to receive $1000 in 5 years, and the effective annual interest rate during this period is 10% (or 0.10), then the present value of this amount is
For example, assume a given project requires an initial capital investment of $15,000. The project is anticipated to generate revenues of $3,500, $9,400 and $15,100 in the next three years, respectively, and the company's hurdle rate is 7%. The present value of the anticipated income is $3,500 / (1 + 0.07) ^ 1) + $9,400 / (1 + 0.07) ^ 2 + $15,100 / (1 + 0.07) ^ 3, or $23,807. The NPV of this project can be determined by simply subtracting the initial capital investment from the discounted revenue: $23,807 - $15,000 = $8,807.
While the PV value is useful, the NPV calculation is invaluable to capital budgeting. A project with a high PV figure may actually have a much less impressive NPV if a great deal of capital is required to fund it.
For example, if a stream of cash flows consists of +$100 at the end of period one, -$50 at the end of period two, and +$35 at the end of period three, and the interest rate per compounding period is 5% (0.05) then the present value of these three Cash Flows are
Because the value of revenue earned today is higher than that of revenue earned down the road, businesses discount future income by the investment's expected rate of return. This rate, called the hurdle rate, is the minimum rate of return a project must generate for the business to consider investing in it.
Present Value - (PV)
The PV calculation indicates the discounted value of all revenue generated by the project, while the NPV indicates how profitable the project will be after accounting for the initial investment required to fund it.
For example, if you are to receive $1000 in 5 years, and the effective annual interest rate during this period is 10% (or 0.10), then the present value of this amount is
For example, assume a given project requires an initial capital investment of $15,000. The project is anticipated to generate revenues of $3,500, $9,400 and $15,100 in the next three years, respectively, and the company's hurdle rate is 7%. The present value of the anticipated income is $3,500 / (1 + 0.07) ^ 1) + $9,400 / (1 + 0.07) ^ 2 + $15,100 / (1 + 0.07) ^ 3, or $23,807. The NPV of this project can be determined by simply subtracting the initial capital investment from the discounted revenue: $23,807 - $15,000 = $8,807.
While the PV value is useful, the NPV calculation is invaluable to capital budgeting. A project with a high PV figure may actually have a much less impressive NPV if a great deal of capital is required to fund it.
For example, if a stream of cash flows consists of +$100 at the end of period one, -$50 at the end of period two, and +$35 at the end of period three, and the interest rate per compounding period is 5% (0.05) then the present value of these three Cash Flows are
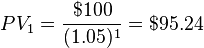

 respectively
respectively
The formula for NPV is:
NPV = Present value (PV) of cash inflows (positive) + present value (PV) of cash outflows (negative)
If NPV is positive, that's good. You can consider the project for selection.
If NPV is negative, it's bad. The project shouldn't be considered for selection.
NPV = Present value (PV) of cash inflows (positive) + present value (PV) of cash outflows (negative)
If NPV is positive, that's good. You can consider the project for selection.
If NPV is negative, it's bad. The project shouldn't be considered for selection.
Internal Rate of Return (IRR) - Project with higher IRR will be selected.
This is the interest rate at which the Net Present Value becomes zero. In other words you can say that it is the rate at which the present value of the outflow is equal to the present value of inflows.
If you have many projects to choose from, you will select the project with the higher IRR.
Opportunity Cost
This is the cost that we are giving up by choosing some other project. If you have many projects, you will chose the project with the lesser opportunity cost.
In certain scenarios we must choose one project and leave the other possible project behind. In this scenario, we might use Opportunity Cost analysis to help us make our decision. For example, assume Project A has a potential net return of $50,000 and Project B has a potential net return of $100,000. But we cannot do them both. The opportunity cost is the amount of profit we will forego opportunity cost by choosing one project over another. Assuming we opportunity cost selected Project B, that means we could not pursue the benefits that Project A offered. Thus, our opportunity cost would be $50,000 - the net amount that Project A would have returned.
Naturally, we want to keep our opportunity costs as low as possible. There will always be opportunity costs when choosing amongst more than one profitable opportunity, but the idea is to minimize that cost as much as possible. This technique is unlikely to be utilized on its own as a project selection tool, but would more likely be used in conjunction with other techniques to help arrive at a decision.
These are the few Benefits Measurement Techniques used in the selection of projects. In general, for most organizations benefits measurement methods are enough to lead them to a decision.
I. The Definition of IRR
Internal rate of return is the interest rate (or discount rate) at which the net present value for the project is zero.
In other words, the rate at which cash inflows equal cash outflows is considered as internal rate of return. It's called "internal rate of return," because there are no other external influences or environmental factors.
As the cash inflows equal cash outflows, for IRR the NPV for the project will be zero. If we put it mathematically, the equation would be:
NPV = 0
=> PV of cash inflows for the project (positive) + PV of cash outflows for the project (negative) = 0
=> PV cash inflows for the project = PV cash outflows for the project
The rate at which present value of cash inflows equals PV of cash outflows will be the IRR. IRR is always noted in percentage terms. To understand, let's look at an example.
An Example of IRR
Your organization has an investment of $100,000 for a project. After one year you will get $110,000 in return. Calculate the IRR.
Present value (PV) of cash outflows for the project = $100,000
Future Value (FV) of cash inflows for the project = $110,000
It's called future value, because we'll get the money after one year.
Therefore, PV of cash inflows for the project = $110,000/(1+R), where R is the rate of return or discounted rate.
For IRR, the value of NPV is zero.
=>PV of cash inflows = PV cash outflows
=> $110,000/(1+R) = $100,000
=> 1 + R = $110,000/$100,000
=> R = ($110,000/$100,000) - 1 = $10,000/$100,000 = 1/10
Or R in percentage terms = (1/10) * 100 = 10%
The IRR for the project is 10 percent.
Let's say you've received the capital of $100,000 at a rate of 12 percent from the investor. After all, someone -- internal or external -- will need to invest in the project. That investor will be expecting a return out of it. This rate is called Cost of Capital (CoC) in accounting terms, because there's a cost associated with it. You have to provide a return for this capital.
However, as you found out above, your IRR is coming at 10 percent, while your CoC is at 12 percent. Will you go for the project? Obviously not. You wouldn't be making any money out of it by executing this project. This leads us to an important conclusion in project selection while using IRR.
If IRR is greater than the desired cut-off rate (or CoC), then you will go ahead with the project.
If IRR is less than the desired cutoff rate (or CoC), then you won't proceed.
II. Ways to Calculate IRR
IRR can be calculated in two ways: for uniform cash flows and for non-uniform cash flows.
II.1: IRR Calculation for Uniform Cash Flows
In the previous example, I showed a simple project with a one-time investment. However, for uniform cash inflows -- a series of cash flows that's uniform year after year, IRR is calculated considering the annuity discount factor.
The formula for annuity discount factor is:
Project investment = Annual net cash flow * Annuity discount factor
=>Annuity discount factor = Project investment/Annual net cash flow
Annuity is a fixed sum of money to be paid every year as a series of payments. (This is another accounting term.)
Once the annuity discount factor is calculated, annuity table is referred to find IRR. Annuity tables are available on accounting sites. If this topic surfaces on your exam, it'll probably reference the present value of annuity factors.
Example 2: Annuity Factors
For this example, I've modified the first example. You have a $100,000 investment for a project. After one year you expect $110,000 in return. Find out the IRR with the help of the annuity factor.
The annuity factor table is given below.
Annuity discount factor = Project investment/Annual net cash flow
=> Annuity discount factor = $100,000/$110,000
=> Annuity discount factor = 10/11 = 0.9090 = 0.9091(approx.)
Looking at the above annuity discount factor table (given in the question), we have a rate of 10 percent for an annuity factor of 0.9091. So the IRR for this project is 10 percent.
Now, let us change this example a bit, to examine annual uniform cash flow.
Example 3: Annual Uniform Cash Flow
You have a $100,000 investment for a project. The expected return on the project in its useful life is $125,000. The useful life of the project is five years. The cash inflow is expected to be uniform. Find out the IRR. The annuity table is shown below.

Here, the cash flow is uniform. Considering the cash inflows and cash outflows, we have the following table. As we have $125,000 over a period of five years, for each year the cash inflow will be $25,000. Note that cash inflows are mentioned as positive, whereas cash outflows (investment) are negative.
Hence, Annuity Discount Factor = Project Investment/Annual Net Cash flow
= $100,000/$25,000
= 100/25 = 4, which is close to 3.9927.
For the annuity discount factor of 3.9927, looking up the table shown in the question, the rate comes out to be at 8 percent. Hence IRR for the project is 8%.
II.2: IRR Calculation for Non-uniform Cash FlowsFor non-uniform or uneven cash flow, we have to calculate the IRR in a different way. First, we need to find out the average cash flow in a year, from which we derive the annuity discount factor. Then, looking up the annuity table, we get an approximate value of IRR. From there, by trial and error and interpolation, the final IRR is derived.
In an uneven cash flow scenario, the formula for IRR is:

It doesn't matter if you have NPV or PV in the denominator. The final value of IRR will remain the same. Both formulas above are correct for IRR.
It's unlikely that you'll have questions about this in the PMP exam. But I've put the formula in in case you're wondering what happens if there's uneven cash flow.
III. IRR for Mutually Exclusive ProjectsIRR can be used to make selection decision between two or more independent projects. The general rule followed for IRR: The higher the better. In other words, all other things being equal, the project with the highest IRR should be selected. Let's take another example to understand this concept.
Example 4: Choosing Between Projects based on IRR
There are four projects before the selection committee, out of which only one can be selected. The IRR for each project is shown below. Which one will be chosen?
Answer:
The project with the highest IRR will be chosen. Above, that’s project B with an IRR of 42 percent.
However, there’s a note of caution when mutually exclusive projects are involved. If both NPV and IRR are present, it’s a good idea to look for NPV as well. A project with higher IRR but lower NPV wouldn’t be preferable over a project with a lower IRR but higher NPV.
To illustrate, here’s an example.
Example 5: IRR and NPV
There two projects, A and B, with the following cash flows. The discount rate is at 10 percent. Which project should be selected?
For project A, NPV = - $1,000 + $2,100 = $1,100
For project A, we have to make NPV zero to find out IRR.
=> - $1,000 + [($2,100)/(1+IRR)] = 0
=> 1 + IRR = 2,100/1,000 = 2.1 => IRR = 2.1 – 1 = 1.1
=> IRR = 110%
Above, I have applied the simple formula, as outlined before, to calculate the IRR. I can also look at the annuity table to derive the IRR.
For project B, we have to make NPV zero to find out IRR.
=> - $10,000 + [($15,000)/(1+IRR)] = 0
=> 1 + IRR = 15,000/10,000 = 1.5 => IRR = 1.5 – 1 = 0.5
=> IRR = 50%
Now, which one to choose?
• Project A higher IRR (110%), but lower NPV ($1,100)
• Project B lower IRR (50%), but higher NPV ($5,000)
Project B will be selected as it gives maximum value to the stakeholders or has higher wealth maximization.
Finally, let us look at the advantages and disadvantages of IRR to have needed understanding on it for the PMP exam.
IV. Advantages and Disadvantages for IRR: